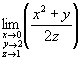|
ТЕКСТ КОНТРОЛЬНОЙ РАБОТЫ
ПО ПРЕДМЕТУ “МАТЕМАТИКА”
Задание 1 Вопрос 1. Что такое матрица?
число;
таблица;
вектор;
функция;
нет правильного ответа.Вопрос 2. Что означают числа
в индексе у элементов матрицы?
степень;
номер строки и столбца;
порядок матрицы;
числа, на которые нужно последовательно умножить элемент;
нет правильного ответа.Вопрос 3. Сколько свойств
определителей Вам известно?
0;
5;
1;
2;
3.Вопрос
4. Что означает запись размер матрицы (2х4)?
матрица нулевая;
матрица квадратная;
матрица имеет две строки и 4 столбца;
определитель матрицы равен 24;
нет правильного ответа.Вопрос 5. Изменится ли
определитель второго порядка, если его строки поменять местами с
соответствующими столбцами ?
нет
да
да, если один из элементов какой-либо строки равен 0
верны ответы 2 и 3
нет правильного ответа
Задание 2
Вопрос 1. Что такое минор М11 для матрицы
(3х3)?
- определитель, получающийся, если вычислить определитель нашей
матрицы, вычеркнув первую строку и первый столбец;
- определитель, равный нулю;
- определитель, получающийся, если вычислить определитель нашей
матрицы, вычеркнув вторую строку и третий столбец;
- определитель, получающийся, если вычислить определитель нашей
матрицы, вычеркнув вторую строку и третий столбец, взятый со знаком
минус;
- нет правильного ответа.
Вопрос 2. Как получить
М23?
- умножить матрицу на два;
- вычислить определитель матрицы, вычеркнув 1-ю строку и первый
столбец;
- нет правильного ответа;
- вычислить определитель, полученный при вычеркивании второй строки
и третьего столбца.
- все ответы верны
Вопрос 3. Что такое алгебраическое
дополнение?
Мji;
Aiк =(-1)i+к Мiк;
определитель матрицы;
порядок матрицы;
нет правильного ответа.Вопрос 4. Отметьте формулу
разложения определителя 3-го порядка по второй строке?
D=а11А11 + а12
А12 +а13А13;
D=а21А21 + а22
А22 +а23А23;
D=а21А13 + а22
А23 +а31А33;
D=а11А23 + а12
А13 +а12А33;
нет правильного ответа.Вопрос 5. Можно ли разложить
определитель четвертого порядка по первой строке?
нет;
если 1-й элемент не равен 0;
иногда;
нет правильного ответа;
да.
Задание 3 Вопрос 1. Можно ли сложить матрицы А (2х3) и
В (2х3)?
- нет;
- да;
- только, если все элементы матрицы В=1;
- иногда;
- нет правильного ответа.
Вопрос 2. Можно ли сложить
матрицы А(2х3) и В(3х4)?
да;
нет;
всегда;
иногда;
нет правильного ответа.Вопрос 3. Какая матрица
называется квадратной?
матрица, у которой число строк равно числу столбцов;
симметрическая;
матрица, у которой число строк больше числа столбцов;
матрица, у которой число строк меньше числа столбцов;
нет правильного ответа.Вопрос 4. Можно ли умножить
матрицу А(2х2) на число С?
нет;
да, но только если с=0;
да, при этом определитель увеличится в С раз ;
нет корректного ответа.
да.Вопрос 5. Можно ли вычесть матрицу А(2х3) из
матрицы В(2х3)?
нет;
всегда;
иногда;
все ответы верны
нет правильного ответа.
Задание 4 Вопрос 1.Что такое нуль – матрица?
- прямоугольная матрица;
- матрица, все элементы которой – нули;
- матрица, на главной диагонали которой находятся нули;
- единичная матрица;
- нет правильного ответа.
Вопрос 2. Можно ли
перемножить матрицы А(2х2) и В(2х2)?
нет;
да;
только, если все элементы матрицы А=0;
иногда;
нет правильного ответа.Вопрос 3. Можно ли
перемножить матрицы А(3х4) и В(4х2)?
да;
нет;
только, если все элементы матрицы В=1;
иногда;
нет правильного ответа.Вопрос 4. Можно ли
перемножить матрицы А(2х3) и В(4х2)?
да;
нет;
всегда;
иногда;
нет правильного ответа.Вопрос 5. Приведите пример
единичной матрицы. Укажите ее порядок.
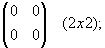
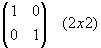 или второго
порядка; или второго
порядка;
 или третьего
порядка; или третьего
порядка;
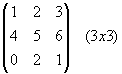 или третьего порядка;
нет правильного ответа. или третьего порядка;
нет правильного ответа.
Задание 5 Вопрос 1. Изменится ли квадратная матрица
А(3х3), если ее умножить на единичную матрицу?
- да;
- она станет единичной;
- она станет нулевой;
- нет;
- нет правильного ответа.
Вопрос. 2. Чему равен
определитель единичной матрицы?
0;
1;
2;
3;
18.Вопрос
3. Что значит транспонировать матрицу?
обнулить;
элемент с номером ij поместить на место ji и наоборот;
умножить на матрицу Е;
элементы с номером ii положить равными нулю
элементы с номером ii положить равными 1.Вопрос 4.
Как обозначаются элементы транспонированной матрицы?
вij-1;
l вij;
в*ij;
5 вij;
нет правильного ответа.Вопрос 5. Чему равно
произведение А·А-1?
- 0;
- Е;
- А+А;
- А*.
- нет правильного ответа
Задание 6. Вопрос 1. Можно ли найти обратную матрицу,
для матрицы, имеющей D=0?
можно;
нет;
всегда;
иногда;
нет правильного ответа.Вопрос 2. Что такое матрица
системы?
нулевая матица;
матрица Е;
матрица, состоящая из коэффициентов свободных членов;
нет правильного ответа;
матица, состоящая из коэффициентов левой части.Вопрос 3. Что такое матичное уравнение?
равенство вида ах2+вх+с=0;
равенство вида А·Х=С, где А,Х,С – матрицы;
равенство вида у=кх+в;
равенство вида 2+18=2;
нет правильного ответа.Вопрос 4. Можно ли решить
систему уравнений матричным способом, если определитель матрицы системы
равен нулю?
да;
нет;
всегда;
иногда;
нет правильного ответа.Вопрос 5. Что такое
определитель системы второго порядка?
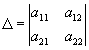 ; ;
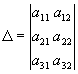 ; ;
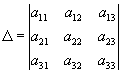 ; ;
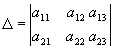 ;
нет правильного ответа. ;
нет правильного ответа.
Задание 7. Вопрос 1. Как записать разложение по ортам
вектора 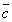 ,
соединяющего точки А(3; 5;7) и В(5;9;12)? ,
соединяющего точки А(3; 5;7) и В(5;9;12)?
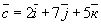 ; ;
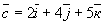 ; ;
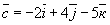 ; ;
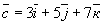 ; ;
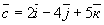 Вопрос 2. Когда вектора 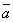 и и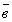 коллинеарны?
коллинеарны?
когда 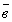 =0;
когда =0;
когда 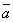 =0;
скалярное произведение этих векторов равно 0;
когда =0;
скалярное произведение этих векторов равно 0;
когда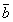 =l =l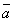 ;
нет правильного ответа.Вопрос 3. В каком случае
вектора называются линейно независимыми? ;
нет правильного ответа.Вопрос 3. В каком случае
вектора называются линейно независимыми?
Если они - коллинеарные;
если равенство  =0 возможно лишь при l1= l2 =…=0;
возможно, если хоть один из коэффициентов l1,…lк =0 возможно лишь при l1= l2 =…=0;
возможно, если хоть один из коэффициентов l1,…lк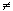 0;
нулевые;
нет правильного ответа.Вопрос 4. Какое выражение
называется линейной комбинацией векторов? 0;
нулевые;
нет правильного ответа.Вопрос 4. Какое выражение
называется линейной комбинацией векторов?
в=0;
 = = а=(с,d)
а-в=d
нет правильного ответаВопрос 5. Могут ли четыре
вектора на плоскости быть линейно независимы?
а=(с,d)
а-в=d
нет правильного ответаВопрос 5. Могут ли четыре
вектора на плоскости быть линейно независимы?
да;
всегда;
иногда;
нет правильного ответа.
нет.
Задание 8 Вопрос 1. Могут ли четыре вектора в
трехмерном пространстве быть линейно независимы?
- да;
- нет;
- всегда;
- иногда;
- нет правильного ответа.
Вопрос 2. Являются ли
векторы–орты 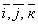 компланарными? компланарными?
нет;
да;
всегда;
иногда;
нет ответа.Вопрос 3. Может ли векторное произведение
векторов 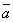 и и 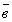 лежать в плоскости,
образованной этими векторами, если оно не равно нулю? лежать в плоскости,
образованной этими векторами, если оно не равно нулю?
да;
всегда;
иногда;
нет правильного ответа.
нет.Вопрос 4. Что изменится в векторном
произведении, если изменить порядок перемножаемых векторов?
Порядок компонент (координат) вектора–произведения;
знаки компонент вектора-произведения;
модуль синуса угла между перемножаемыми векторами;
длина вектора-результата;
нет правильного ответа.Вопрос 5. Что Вы можете
сказать о координатах векторов 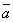 и и 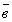 , если они
коллинеарны? , если они
коллинеарны?
они равны нулю;
их координаты пропорциональны;
они положительны;
они отрицательны;
нет правильного ответа.
Задание 9 Вопрос 1. Смешанное произведение это вектор
или скаляр (то есть число)?
- вектор;
- скаляр;
- матрица;
0;
нет правильного ответа.Вопрос 2. Скалярное
произведение – это число или вектор?
число;
вектор;
вектор и число;
0;
1;Вопрос
3. Векторное произведение – это число или вектор?
число;
вектор;
вектор и число;
0;
1;Вопрос
4. Чему равен модуль (длина) векторного произведения 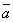 и и 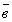 ? ?
площади параллелограмма, построенного на векторах, как на
сторонах;
0;
1;
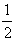 модуля
вектора модуля
вектора 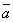 ;
2.Вопрос
5. Чему равен модуль смешанного произведения векторов ;
2.Вопрос
5. Чему равен модуль смешанного произведения векторов 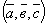 ? ?
0;
объему параллелепипеда, построенного на векторах 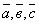 ;
1;
объему пирамиды, построенной на векторах ;
1;
объему пирамиды, построенной на векторах 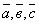 ;
нет правильного ответа ;
нет правильного ответа
Задание 10 Вопрос 1. Приведите уравнение прямой на
плоскости с угловым коэффициентом?
- х
2 +у=0;
х2+у2=5;
у-у0=3(х-х0);
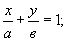 у=кх+ в;Вопрос 2. Верно ли, что уравнение второй
степени задаёт прямую на плоскости ?
у=кх+ в;Вопрос 2. Верно ли, что уравнение второй
степени задаёт прямую на плоскости ?
да;
нет;
всегда;
иногда;
нет правильного ответа.Вопрос 3. Приведите уравнение
пучка прямых, проходящих через точку (х0,
у0).
у=кх+в;
у-у0 =к (х-х0);
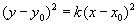 3х=5у+2
нет правильного ответаВопрос 4. Приведите уравнение
прямой, содержащее координаты двух точек, через которые она проходит.
3х=5у+2
нет правильного ответаВопрос 4. Приведите уравнение
прямой, содержащее координаты двух точек, через которые она проходит.
 ;
у=кх+в;
х2 +2у=0;
у=2х+3;
нет правильного ответа.Вопрос 5.Приведите общее
уравнение прямой на плоскости. ;
у=кх+в;
х2 +2у=0;
у=2х+3;
нет правильного ответа.Вопрос 5.Приведите общее
уравнение прямой на плоскости.
у=3х+2;
Ах+Ву+С=0;
у=2х+3;
х2+у2=5;
нет правильного ответа.
Задание 11 Вопрос 1. Приведите каноническое уравнение
прямой на плоскости.
- х=2;
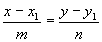 , где (m,n)
– направляющий вектор; , где (m,n)
– направляющий вектор;
- у=2х;
- у=5;
- нет правильного ответа.
Вопрос 2. Приведите общее
уравнение плоскости в пространстве.
2х2+3у+Z+5=0;
Ах+Ву+СZ+D=0;
Ах+Ву+С=0;
Z=0;
нет правильного ответа.Вопрос 3. Приведите уравнение
плоскости, проходящей через три заданные точки А(х1у1z1) А(х2у2z2) А(х3у3z3).
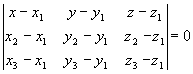 ; ;
- Ах+Ву+СZ+D=0;
- Z=5;
- х+у-z=0;
- нет правильного ответа.
Вопрос 4. Приведите
каноническое уравнение прямой, проходящей через точку М0(х0у0z0) и
имеющей направляющий вектор L(Lx,Lу,Lz).
у=х –L;
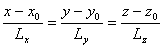 ; ;
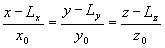 ;
х - Lx +y - Lу +z -
Lz =0;
нет правильного ответа.Вопрос 5. Являются ли
плоскости 2х+3у+7Z+5=0 и 10х+15у+7Z+5=0 параллельными? ;
х - Lx +y - Lу +z -
Lz =0;
нет правильного ответа.Вопрос 5. Являются ли
плоскости 2х+3у+7Z+5=0 и 10х+15у+7Z+5=0 параллельными?
да;
нет;
иногда;
только при определенных значениях переменных;
нет правильного ответа.
Задание 12 Вопрос 1. Отметьте каноническое уравнение
окружности.
- у=кх+в;
- (х-х0)2+(у-у0)2=R2;
- у=5;
- у=coust=C;
- нет правильного ответа.
Вопрос 2. Выпишите
каноническое уравнение эллипса.
у2+2х+у0=0;
(х-х0)(у-у0)=0;
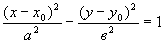 нет правильного ответа;
нет правильного ответа;
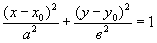 Вопрос 3.
Выпишите каноническое уравнение гиперболы. Вопрос 3.
Выпишите каноническое уравнение гиперболы.
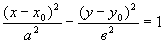 ;
у=2х;
(у-у0)2= (х-х0) 2;
у=0;
нет правильного ответаВопрос 4. Выпишите
каноническое уравнение параболы с директрисой, перпендикулярной Ох. ;
у=2х;
(у-у0)2= (х-х0) 2;
у=0;
нет правильного ответаВопрос 4. Выпишите
каноническое уравнение параболы с директрисой, перпендикулярной Ох.
у=3х+5;
(у-у0)2=2p(х-х0);
у=5;
нет правильного ответа
все ответы верныВопрос 5. Какие прямые являются
асимптотами гиперболы?
у=Z;
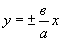 ;
у=5;
х=2;
нет правильного ответа. ;
у=5;
х=2;
нет правильного ответа.
Задание 13 Вопрос 1. Что называется функцией?
- число;
- правило, по которому каждому значению аргумента х в соответствует
одно и только одно значение функции у;
- вектор;
- матрица;
- нет правильного ответа.
Вопрос 2. В каком случае
можно определить обратную функцию?
когда каждый элемент имеет единственный прообраз;
когда функция постоянна;
когда функция не определена;
когда функция многозначна;
нет правильного ответа.Вопрос 3. Какая функция
называется ограниченной?
обратная;
функция f(x) называется ограниченной, если m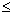 f(x) f(x)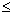 M;
сложная;
функция f(x) называется ограниченной, если f(x)›0;
функция f(x) называется ограниченной, если f(x) M;
сложная;
функция f(x) называется ограниченной, если f(x)›0;
функция f(x) называется ограниченной, если f(x)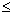 0;Вопрос 4. Какая точка
называется предельной точкой множества А? 0;Вопрос 4. Какая точка
называется предельной точкой множества А?
нулевая;
т.х0 называется предельной точкой множества
А, если в любой окрестности точки
х0 содержатся
точки множества А, отличающиеся от х0;
не принадлежащая множеству А;
нет правильного ответа;
лежащая на границе множества.Вопрос 5. Может ли
существовать предел в точке в том случае, если односторонние пределы не
равны?
да;
иногда;
нет;
всегда;
нет правильного ответа.
Задание 14 Вопрос 1. Является ли функция 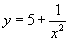 бесконечно малой при бесконечно малой при 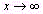 ? ?
- да;
- нет;
- иногда;
- всегда;
- нет правильного ответа.
Вопрос 2. Является ли функция
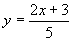 бесконечно большой
при бесконечно большой
при 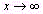 ? ?
да;
нет;
иногда;
если х=0;
нет правильного ответа.Вопрос 3. Является ли функция
у=sin x бесконечно большой при 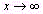 ? ?
да;
нет;
иногда;
всегда;
нет правильного ответа.Вопрос 4. Является ли функция
у=cos x бесконечно большой при 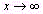 ? ?
да;
нет;
иногда;
всегда;
нет правильного ответа.Вопрос 5. Является ли функция
у=tg x бесконечно большой в т. х0=0?
- да;
- иногда;
- всегда;
- нет;
- нет правильного ответа.
Задание 15 Вопрос 1. Является ли произведение
бесконечно малой функции на функцию ограниченную, бесконечно малой
функцией?
- нет;
- да;
- иногда;
- не всегда;
- нет правильного ответа.
Вопрос 2. В каком случае
бесконечно малые a(х) и b(х) называются бесконечно малыми одного порядка в
точке х0?
если они равны;
если  ;
если ;
если 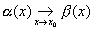 ;
если их пределы равны 0;
нет правильного ответа.Вопрос 3. Сколько видов
основных элементарных функций мы изучили? ;
если их пределы равны 0;
нет правильного ответа.Вопрос 3. Сколько видов
основных элементарных функций мы изучили?
5;
1;
0;
2;
3.Вопрос
4. Чему равен предел константы С?
0;
е;
1;
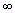 ;
с.Вопрос 5. Является ли степенная функция
непрерывной? ;
с.Вопрос 5. Является ли степенная функция
непрерывной?
нет;
да;
иногда;
при х >1;
нет правильного ответа.
Задание 16 Вопрос 1. Приведите формулу первого
замечательного предела.
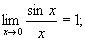
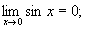
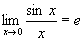 ;
уґ=кх+в;
нет правильного ответа.Вопрос 2. Приведите формулу
второго замечательного предела. ;
уґ=кх+в;
нет правильного ответа.Вопрос 2. Приведите формулу
второго замечательного предела.
0;
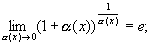
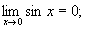
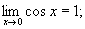
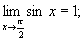 Вопрос 3.
Какие функции называются непрерывными? Вопрос 3.
Какие функции называются непрерывными?
- бесконечно малые;
- удовлетворяющие условиям: а) f определима в т. х0 в)
существует
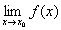 и
равен f(x0); и
равен f(x0);
- бесконечно большие;
- степенные;
- тригонометрические.
Вопрос 4. Если
f(x0+0)=f(x0-0)=L, но f(x0)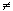 L, какой разрыв имеет функция? L, какой разрыв имеет функция?
нет правильного ответа;
2-го рода;
устранимый;
неустранимый;
функция непрерывна.Вопрос 5. Какой разрыв имеет f(x)
в т. х0, если f(x0-0)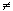 f(x0+0), и не известно: конечны ли эти пределы? f(x0+0), и не известно: конечны ли эти пределы?
устранимый;
неустранимый;
функция непрерывна;
1-го рода;
2-го рода.
Задание 17 Вопрос 1. Сформулируйте свойство
непрерывности сложной функции.
- сложная функция непрерывна всегда;
- если функция u=g(х) непрерывна в точке х0 и функция
у=f(u) непрерывна в точке u=g(х0), то сложная
функция у=f(g(x)) непрерывна в точке х0.
- сложная функция, являющаяся композицией непрерывных функций не
является непрерывной;
- сложная функция разрывна;
- сложная функция является композицией непрерывных функций и имеет
устранимый разрыв.
Вопрос 2. Является ли функция
у=(1-х2)3 непрерывной?
нет;
иногда;
при х >1;
да;
нет правильного ответа.Вопрос3. Что такое
производная функции?
Предел значения этой функции;
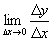 0;
1;
еВопрос 4. Какая функция является дифференцируемой в
точке х=4 ?
0;
1;
еВопрос 4. Какая функция является дифференцируемой в
точке х=4 ?
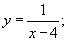 ln(x-4);
имеющая производную в точке х=4 ;
непрерывная в точке х=4;
нет правильного ответаВопрос 5. Какая функция
называется дифференцируемой на интервале (а,в)?
ln(x-4);
имеющая производную в точке х=4 ;
непрерывная в точке х=4;
нет правильного ответаВопрос 5. Какая функция
называется дифференцируемой на интервале (а,в)?
разрывная в каждой точке интервала;
дифференцируемая в каждой точке этого интервала;
постоянная;
возрастающая;
убывающая.
Задание 18 Вопрос 1. Чему равна производная константы
у=с?
1;
0;
е;
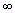 ;
нет правильного ответа.Вопрос 2. Чему равна
производная функции у=х5? ;
нет правильного ответа.Вопрос 2. Чему равна
производная функции у=х5?
- 0;
- 1;
- е;
- 5х
4;
- нет правильного ответа.
Вопрос 3. Чему равна
производная у=ех?
0;
ех;
е;
1;
нет правильного ответа.Вопрос 4. Чему равна
производная у=ln x?
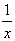 ;
0;
е;
1;
нет правильного ответа.Вопрос 5. Чему равна
производная у=sin x? ;
0;
е;
1;
нет правильного ответа.Вопрос 5. Чему равна
производная у=sin x?
0;
cos x;
е;
1;
нет правильного ответа.
Задание 19 Вопрос 1. Может ли непрерывная функция быть
дифференцируемой?
- нет;
- да;
- только в точке х=
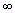 ; ;
- только в точке х=0;
- нет правильного ответа.
Вопрос 2. Всегда ли
непрерывная функция является дифференцируемой?
всегда;
никогда;
не всегда;
в т. х=0;
в т. х=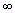 .Вопрос 3. Может ли дифференцируемая функция
быть непрерывной? .Вопрос 3. Может ли дифференцируемая функция
быть непрерывной?
нет;
да;
никогда;
в т. х=0;
в т. х=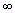 .Вопрос 4. Всегда ли дифференцируемая функция
является непрерывной? .Вопрос 4. Всегда ли дифференцируемая функция
является непрерывной?
не всегда;
никогда;
нет правильного ответа;
в т. х=0;
всегда.Вопрос 5. Найти вторую производную от функции
у=sin x.
cos x;
-sin x;
0;
1;
tg x.
Задание 20 Вопрос 1. Как называется главная, линейная
часть приращения функции?
производная;
дифференциал (dу);
функция;
бесконечно малая;
бесконечно большая.Вопрос 2. Сформулируйте правило
Лопиталя.
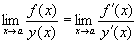 ,если предел правой части
существует; ,если предел правой части
существует;
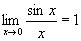 ; ;
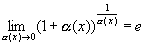 ;
нет правильного ответа; ;
нет правильного ответа;
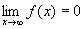
. Вопрос 3. Какие виды
неопределенностей можно раскрыть при помощи правила Лопиталя?
{0};
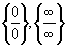 ;
c x 0;
c x ;
c x 0;
c x 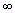 ; ;
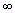 x x 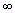 .Вопрос 4. Является ли условие у'=0 в точке,
не являющейся граничной точкой области определения дифференцируемой
функции у, необходимым условием существования экстремума в этой точке? .Вопрос 4. Является ли условие у'=0 в точке,
не являющейся граничной точкой области определения дифференцируемой
функции у, необходимым условием существования экстремума в этой точке?
нет;
да;
не всегда;
иногда;
нет правильного ответа.Вопрос 5. Является ли условие
у'=0 в т. х=а достаточным условием существования экстремума?
да;
нет;
не всегда;
иногда;
нет правильного ответа.
Задание 21 Вопрос 1. Какая функция называется функцией
двух переменных?
- f(x);
- n=f(x,у,z);
- нет правильного ответа;
- z=f(x,у);
- f(x)=const=c.
Вопрос 2. Вычислить предел функции 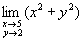 . .
0;
29;
1;
5;
2.Вопрос
3. Вычислить предел функции 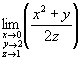
0;
1;
16;
18;
20.Вопрос
4. Какие линии называются линиями разрыва?
прямые;
состоящие из точек разрыва;
параболы;
эллипсы;
нет правильного ответа.
Вопрос 5. Найти первую производную по у от функции z=3x+2у.
- 1;
- 2;
- 0;
- 5;
- нет правильного ответа.
|
 или третьего
порядка;
или третьего
порядка;
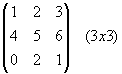 или третьего порядка;
или третьего порядка;
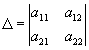 ;
;
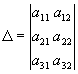 ;
;
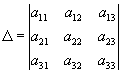 ;
;
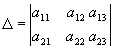 ;
;
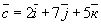 ;
;
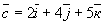 ;
;
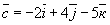 ;
;
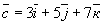 ;
;
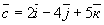
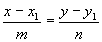 , где (m,n)
– направляющий вектор;
, где (m,n)
– направляющий вектор;
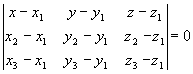 ;
;
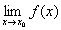 и
равен f(x0);
и
равен f(x0);
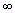 ;
;
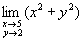 .
.